RCWA電磁界解析ソフト : Wsr
To English
● 1. 計算原理、フーリエ空間のMaxwell方程式
● 2. hm(Harmonics数比)とtrc(切り捨て係数) New 2025/01/19
● 3. 非周期構造に対応する光源、境界条件
● 4. 光源位置、最上面と任意の中間面
● 5. メモリの圧縮
● 6. 遠方界の計算、下面側と上面側
● 7. 光量計測
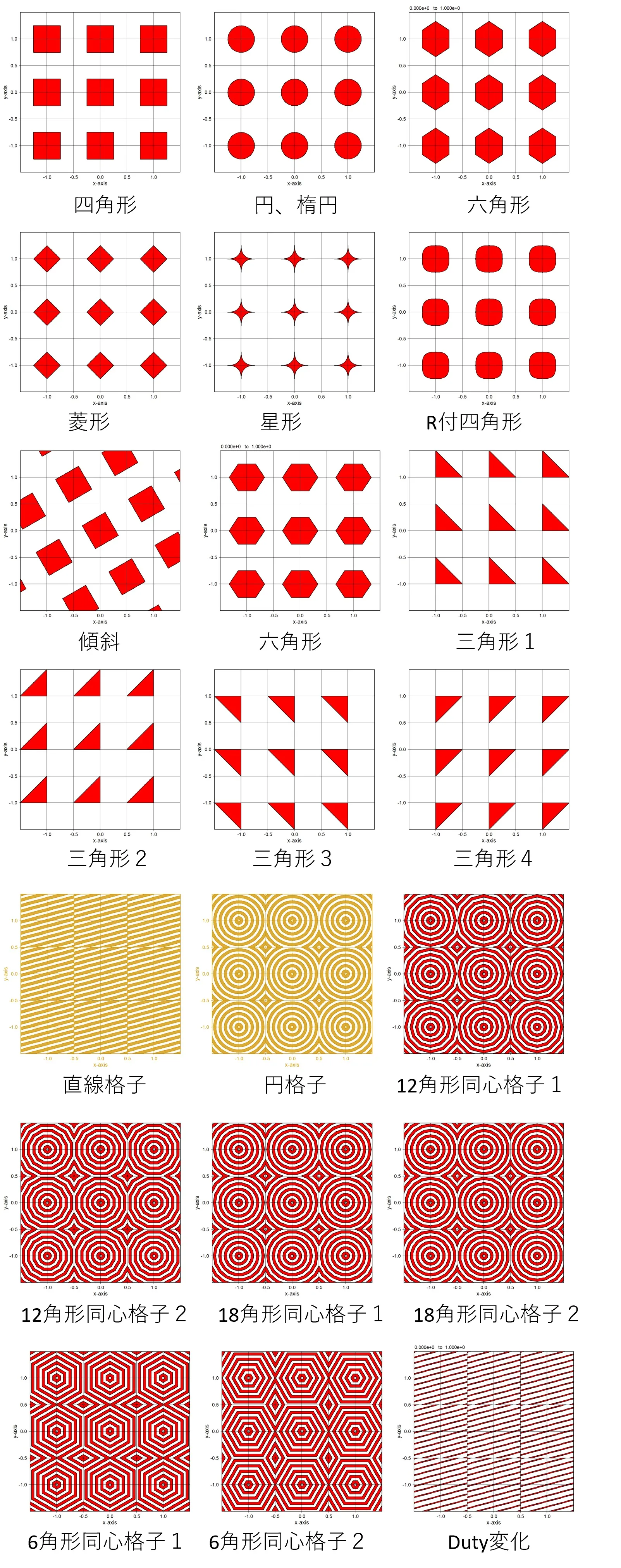
● 8. 多彩な断面構造の表現
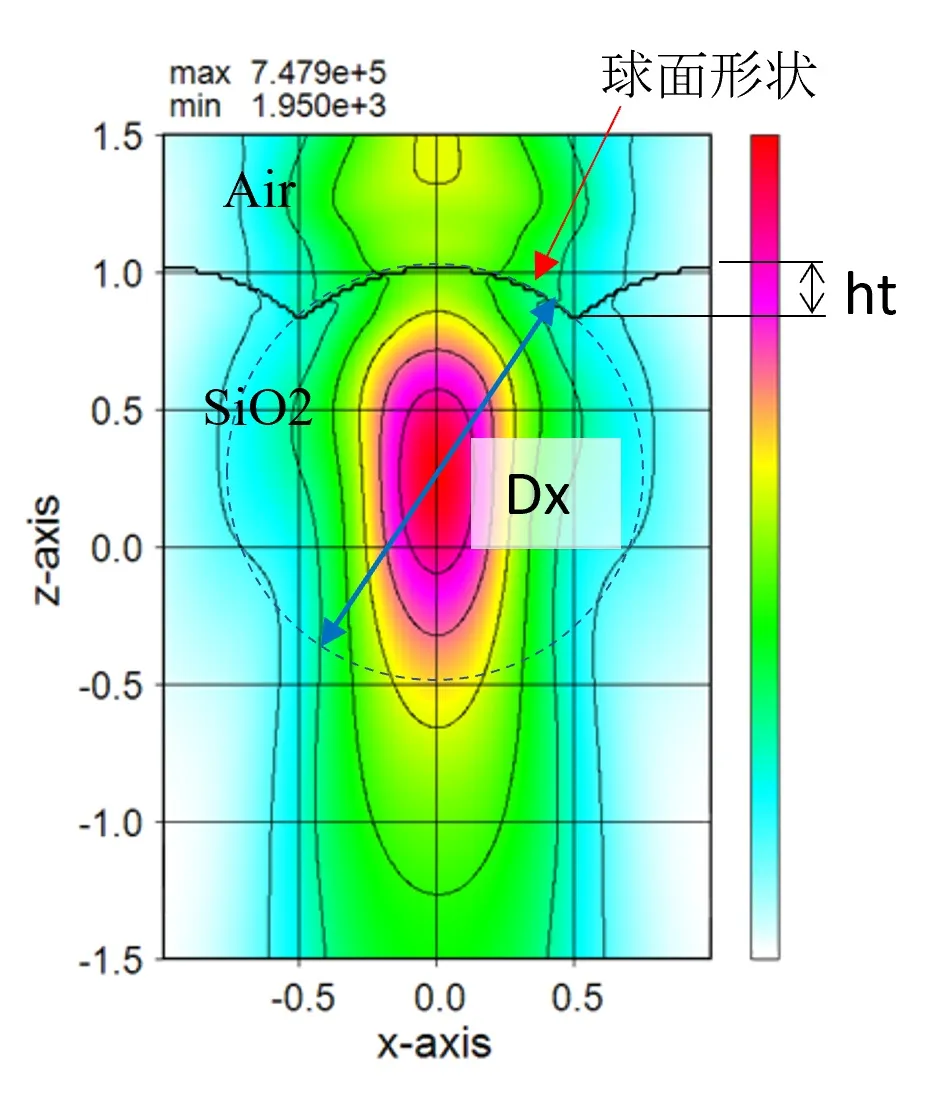
● 9. レンズ集光の計算
● 10. 回折効率の計算
● 11. 計算結果の可視化
● 12. 出力ファイル
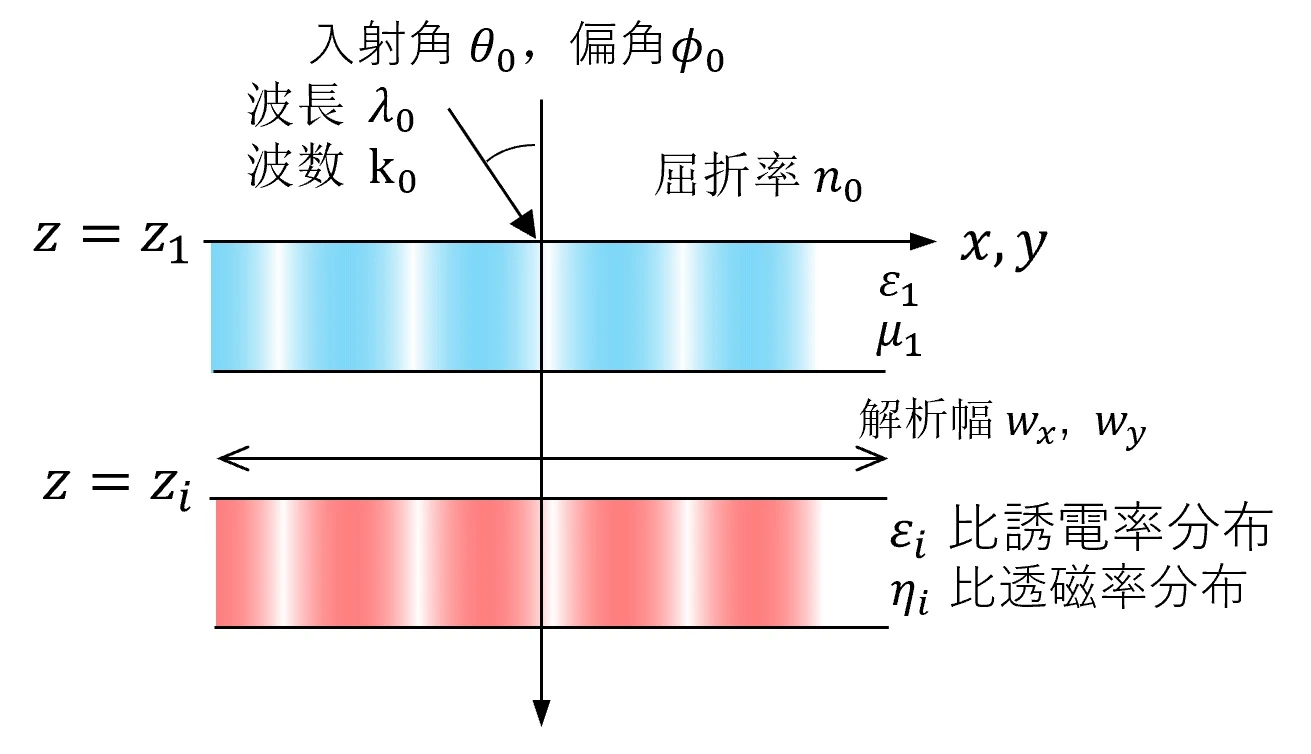
(1) 電磁界vectorと格子matrixの定義
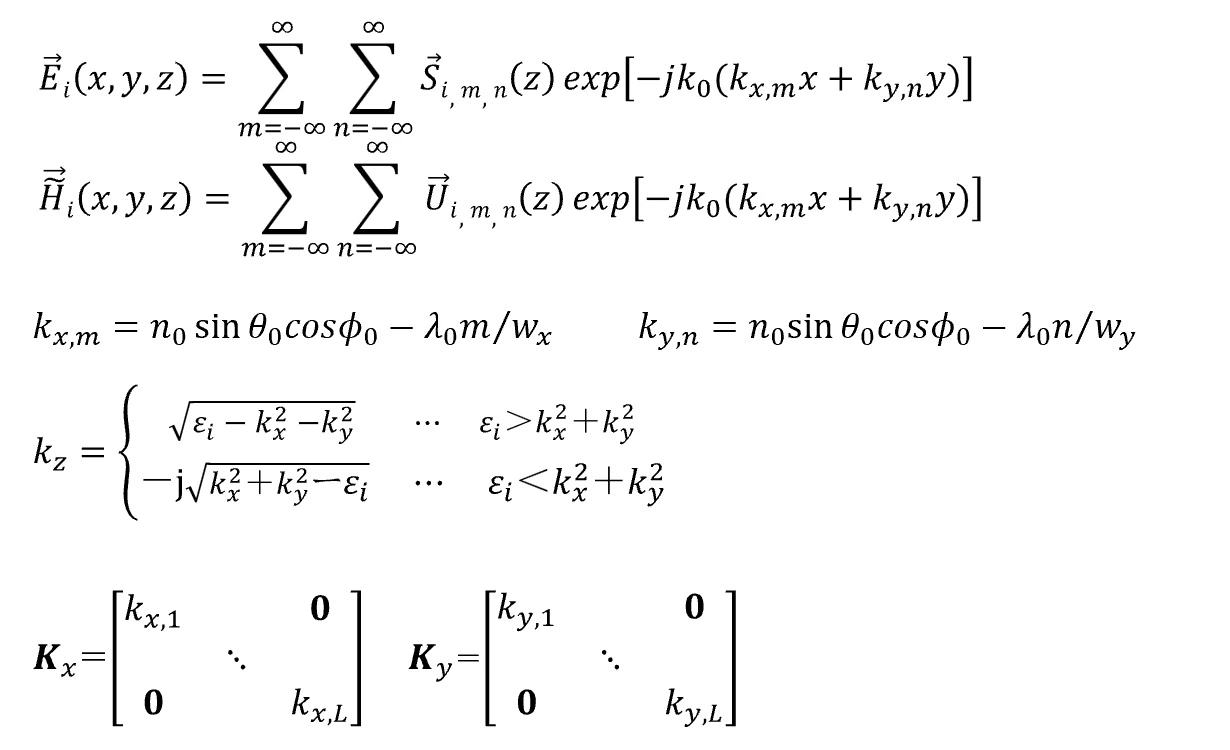
(2) 比誘電率のConvolution matrix計算とmatrixの圧縮
比誘電率分布εi(x,y)の離散フーリエ変換行列の内、中心から(2n+1)×(2n+1)の方形行列を抜き取り、(n+1)2×(n+1)2サイズのConvolution matrixを生成する。抜き取りの形状は円や菱形などに縮小でき、その分Convolution matrixのサイズも大幅に圧縮できる(wsr独自の機能)。wsrではn(Harmonics数)はhm (Harmonics数比)で、抜き取り形状はtrc(切り捨て係数)で設定される。この抜き取りはRCWA法における近似操作に外ならず、計算精度が犠牲になるので演算負荷とのバランスを考慮して決定する必要がある。抜き取りの形状が方形の場合、行列𝑷i, 𝑸i, 𝜴i2, 𝑾iのサイズは2(n+1)2×2(n+1)2となり、波動方程式の行列サイズは4(n+1)2×4(n+1)2になる。演算負荷(メモリ、CPU)は(2n)4に比例する。

(3) 構造matrix計算
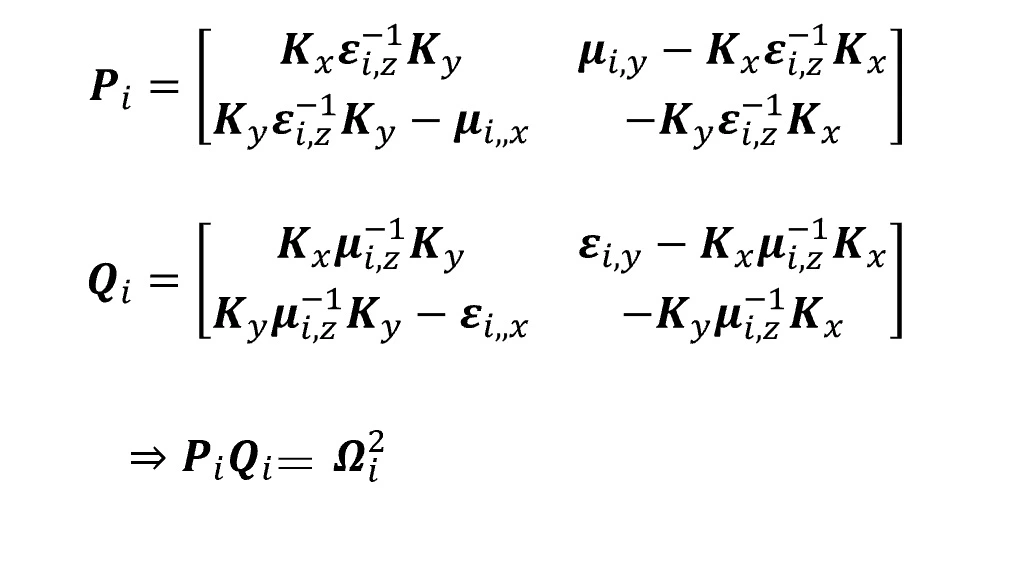
(4) 固有値問題を解く
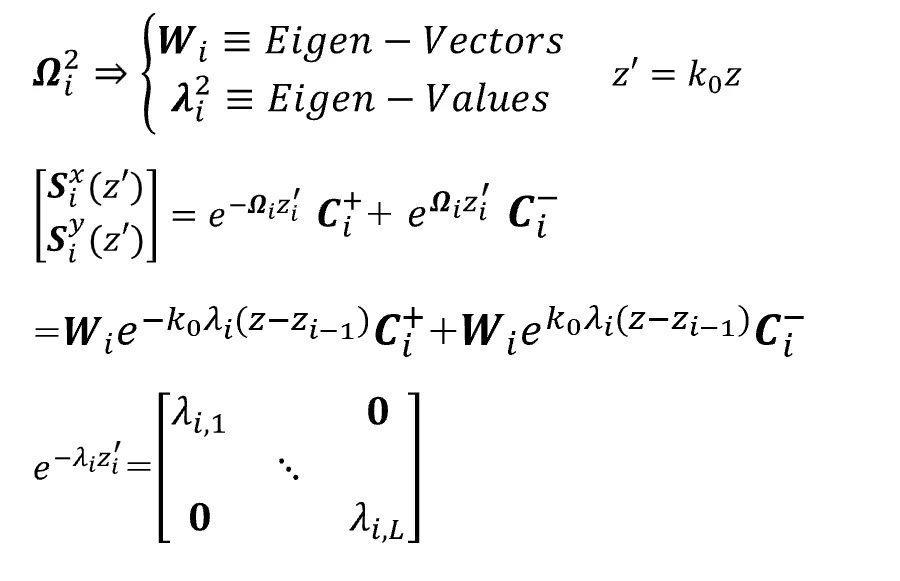
(5) 行列の整列
回折次数を揃えるため固有値λi2の順位を入れ替えて行列を整列させる。
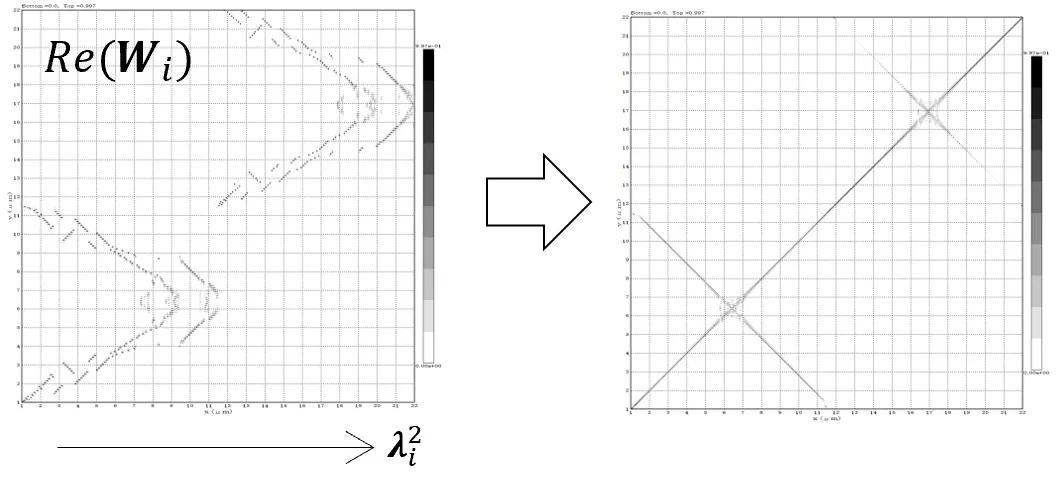
(6) 波動方程式を解く
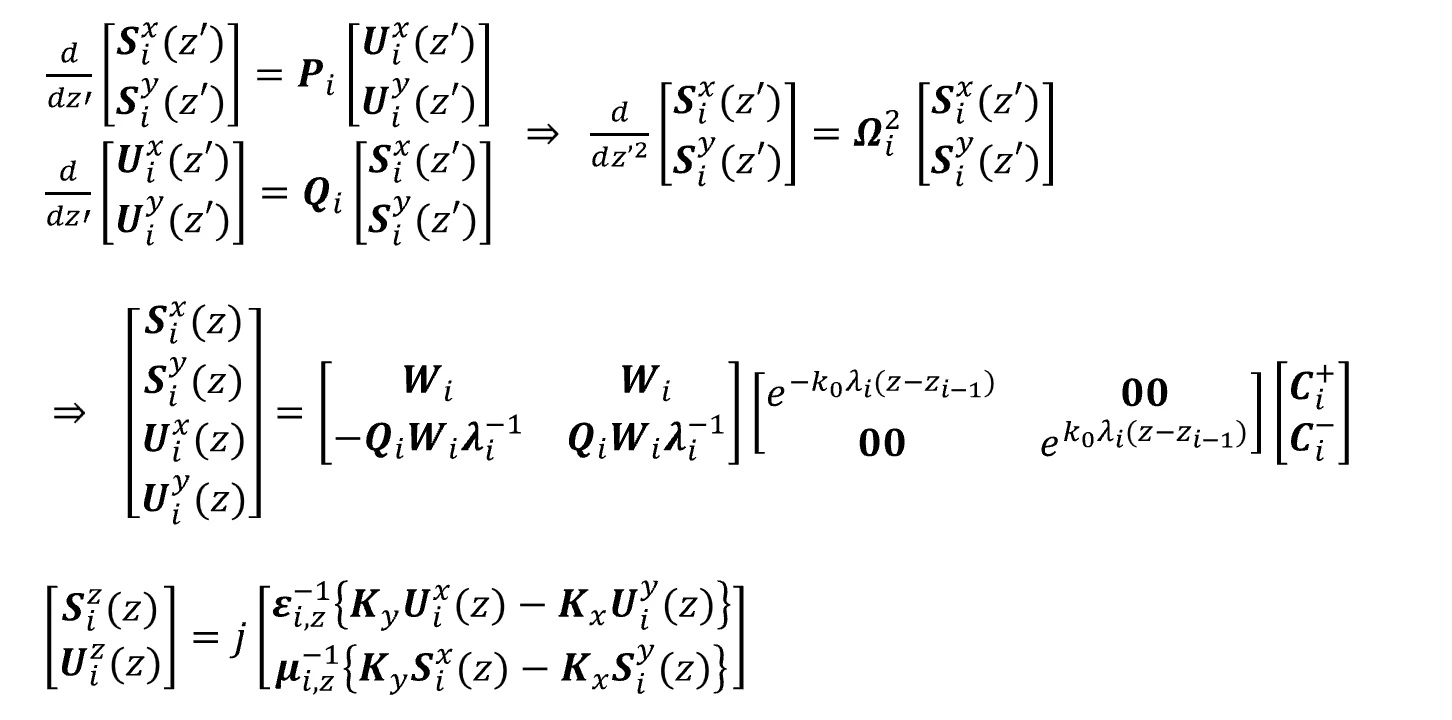
Harmonics数(整数)をn、波長をλ、解析領域の幅をwとすると、Harmonics数比hmはhm=nw/λで定義される。 Convolution matrixの大きさはn、trc(切り捨て係数)により次式で制限される。 |i/n|2*trc+|j/n|2*trc<1.0
hmが大きいほど、またtrcが小さいほど計算精度は向上するがメモリ消費も増大する(購入前はhmは5以下に制限されている)。
(2) hmと解(透過率)の安定性
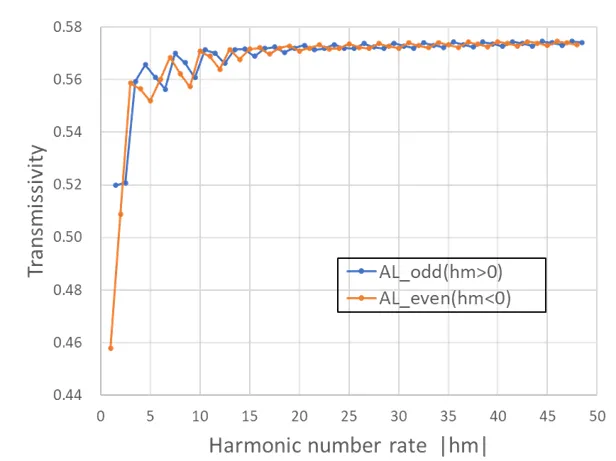
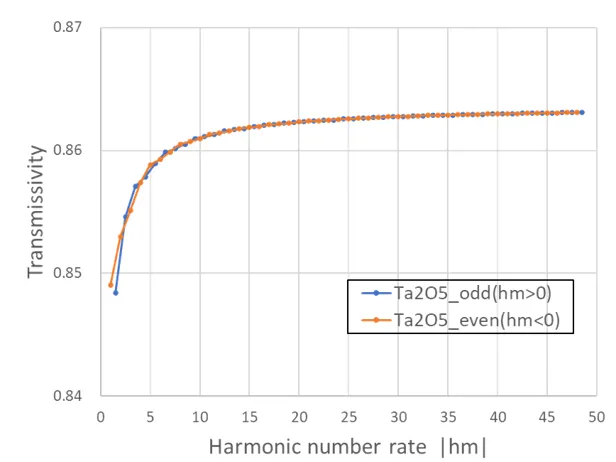
下図はtrcを固定して(trc=1.0)、金属円板のモデルでhmに対する解(透過率)の安定性を示す。hmが5以上で安定するが、Harmonics数nが偶数か奇数かで振る舞いに差があり、偶数の方が安定しているのでWsrでは指定しない限り偶数を選んでいる。
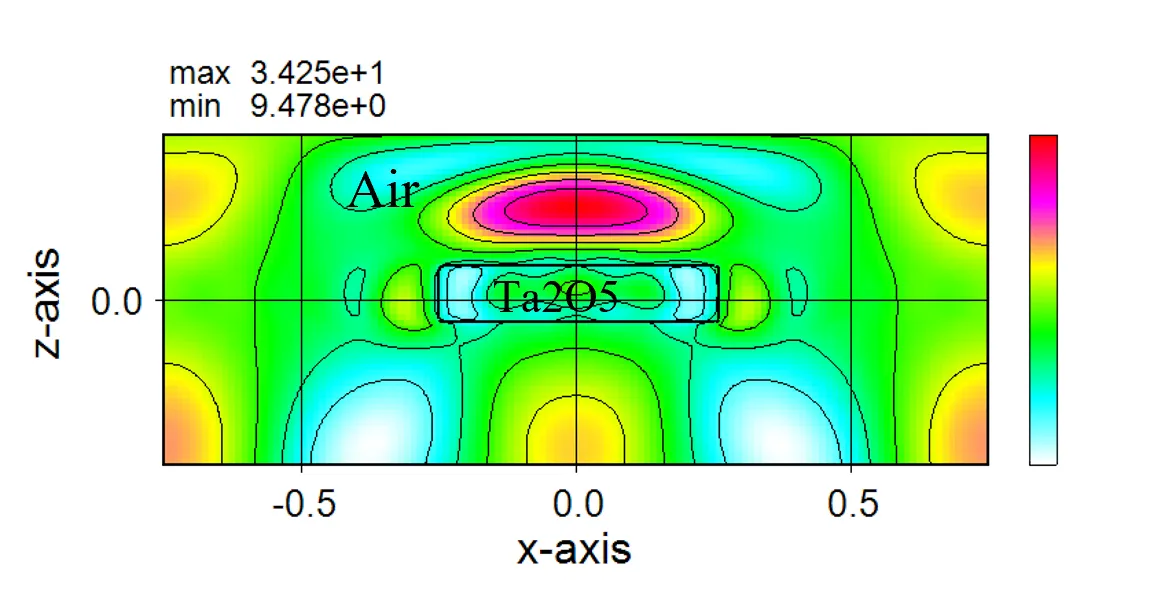
下図はtrcを固定して(trc=1.0)、誘電体円板のモデルでhmに対する解(透過率)の安定性を示す。hmが5以上で安定するが、Harmonics数nが偶数か奇数かの差は小さい。
(3) trcと解(透過率)の安定性
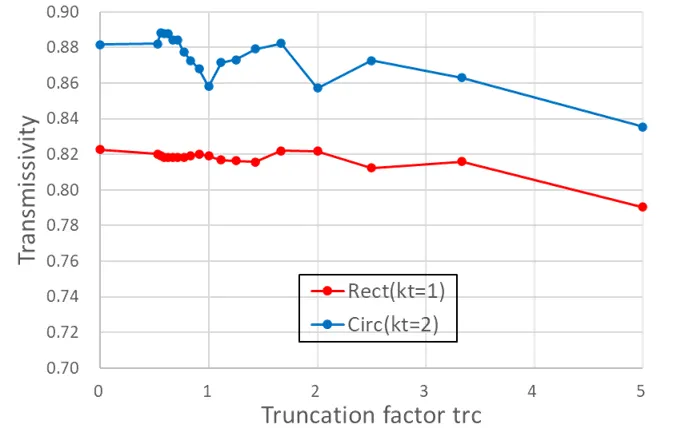
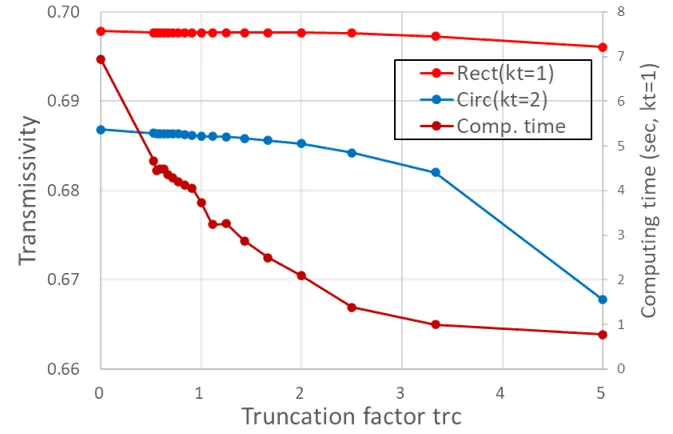
下図はhmを固定して(hm=5.0)、金属の円板と方形板を比較したモデルでtrcに対する解(透過率)の安定性を示す。円では3以下、方形では4以下のtrcで解は安定している。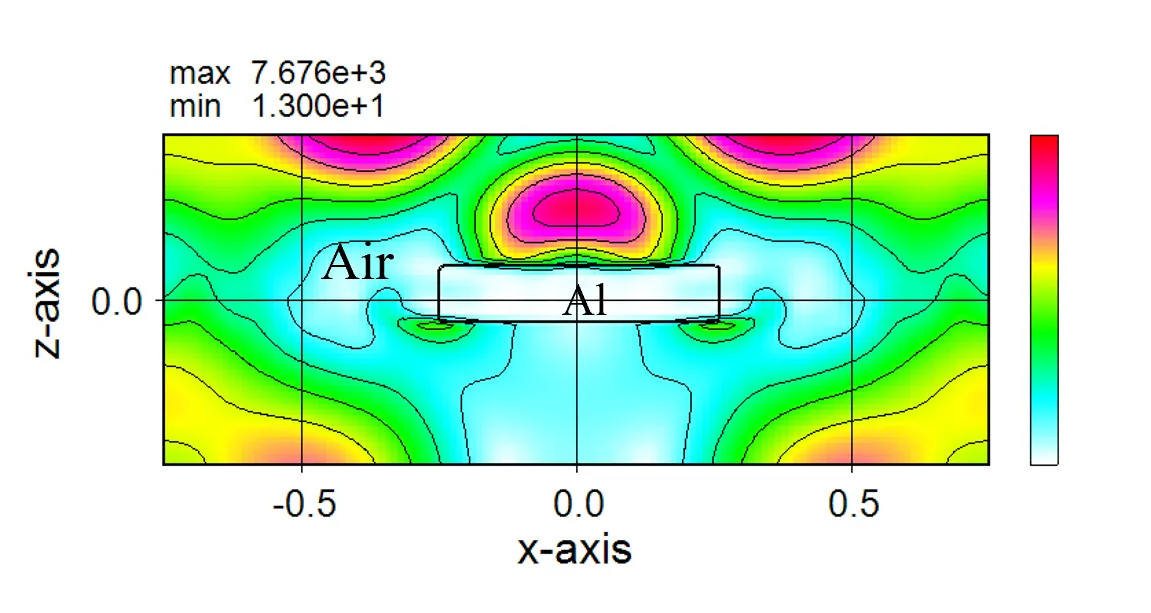
下図はhmを固定して(hm=5.0)、誘電体の円板と方形板を比較したモデルでtrcに対する解(透過率)の安定性を示す。円では3以下、方形では4以下のtrcで解は安定している。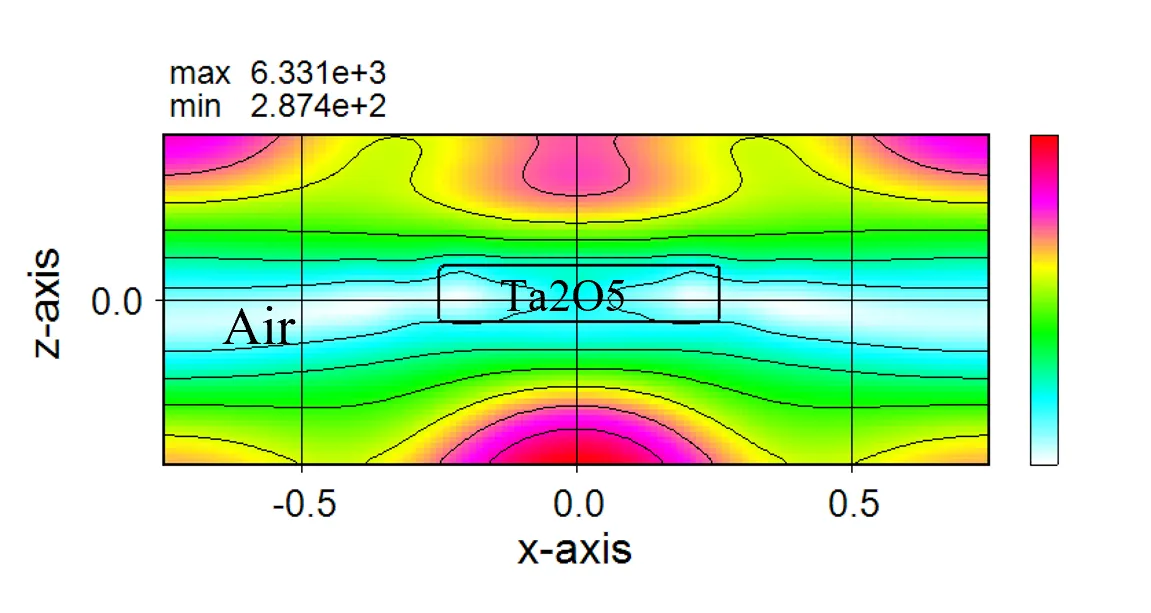
(4) trcとSpatial harmonics分布
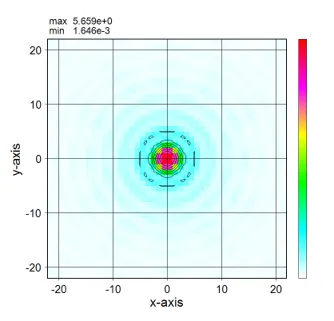
円形の構造に対するSpatial harmonics分布(出力eps.out)は等方的な広がりである。
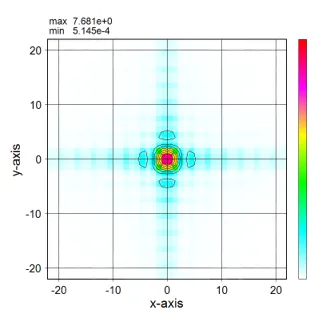
これに対し、方形の構造に対する分布は0度、90度方向に沿って広がる。
従って円形の構造にはtrc=1.0、方形の構造にはtrc=2.0にしても計算精度の劣化は小さく、メモリ消費はそれぞれ0.6倍、0.25倍に圧縮できる。
(5) hmとtrc
hm,trcの設定はConvolution matrixの定義領域を制限するのでRCWA法に於ける近似操作の一つであるが、大幅なメモリ圧縮と演算高速化が可能になる。またhm,trcの適切な設定を行うことで近似誤差を極小化できる。なおtrcによる領域制限はWsr独自の機能であり、市販ソフトの数倍の演算性能を達成できる。
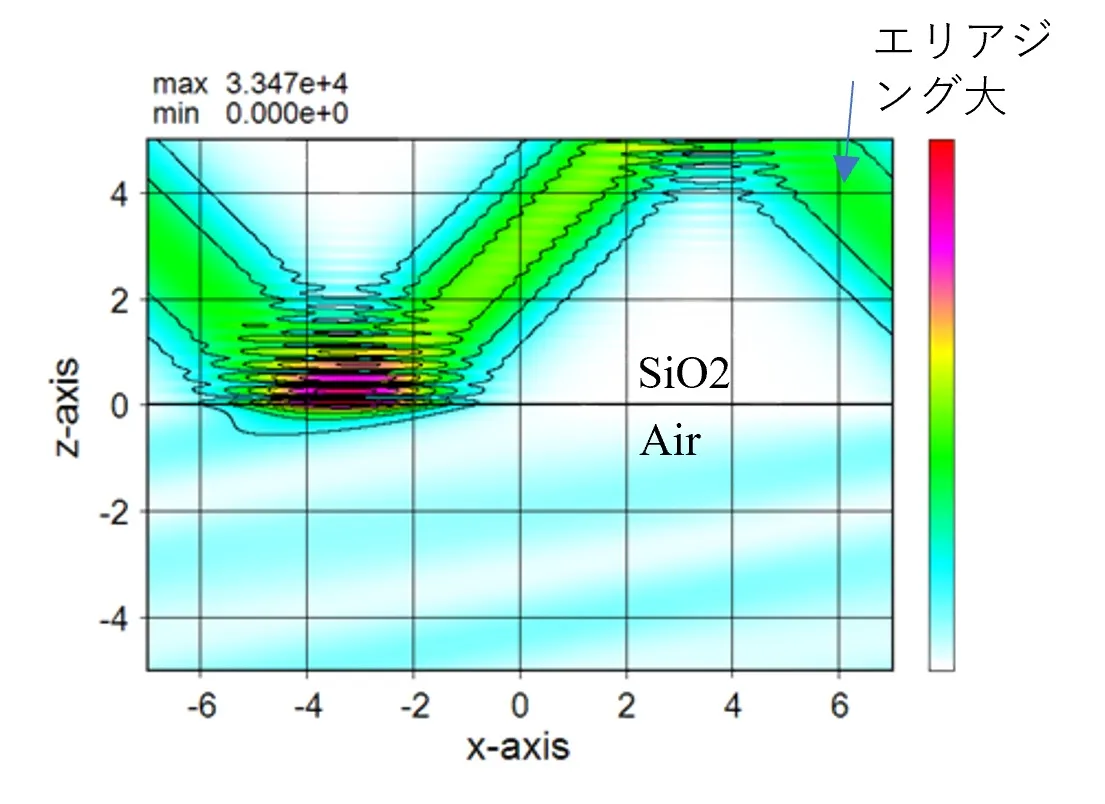
● 分布光源で境界条件が周期境界条件(PBC)の場合。
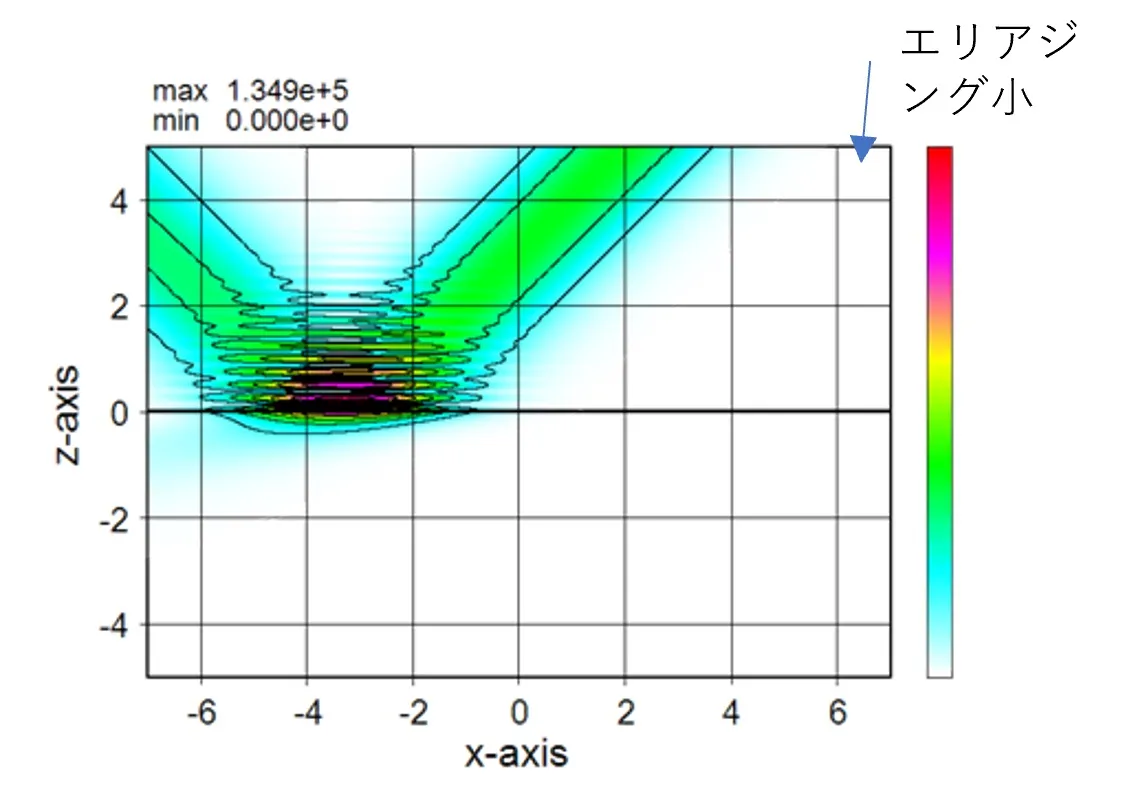
● 分布光源で境界条件が吸収境界条件(ABC)の場合。
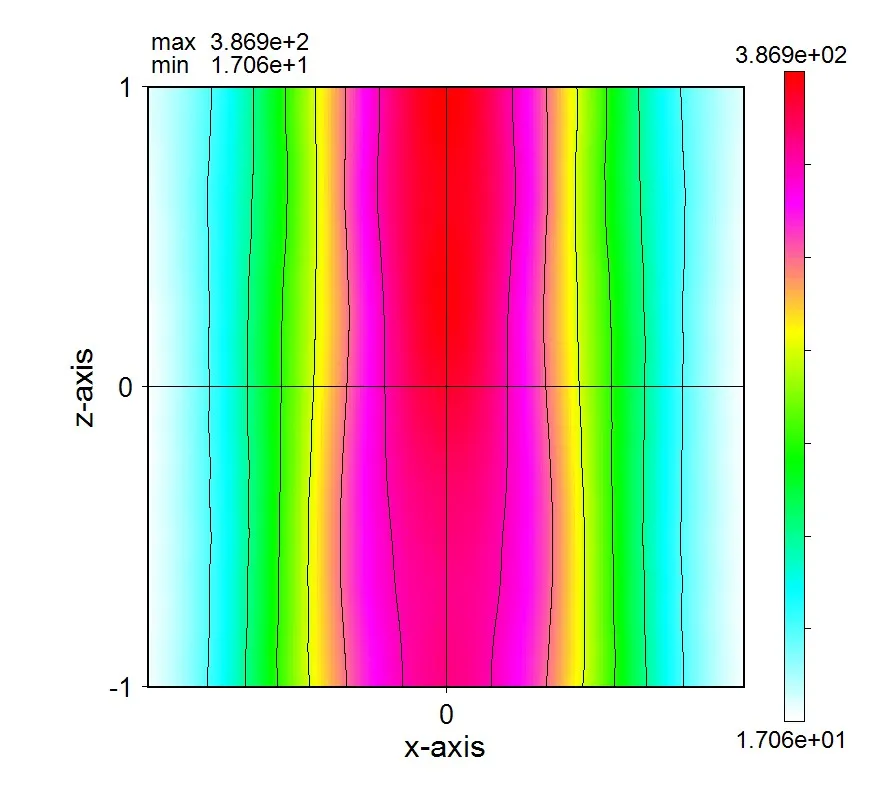
● 光源位置が最上面の場合。
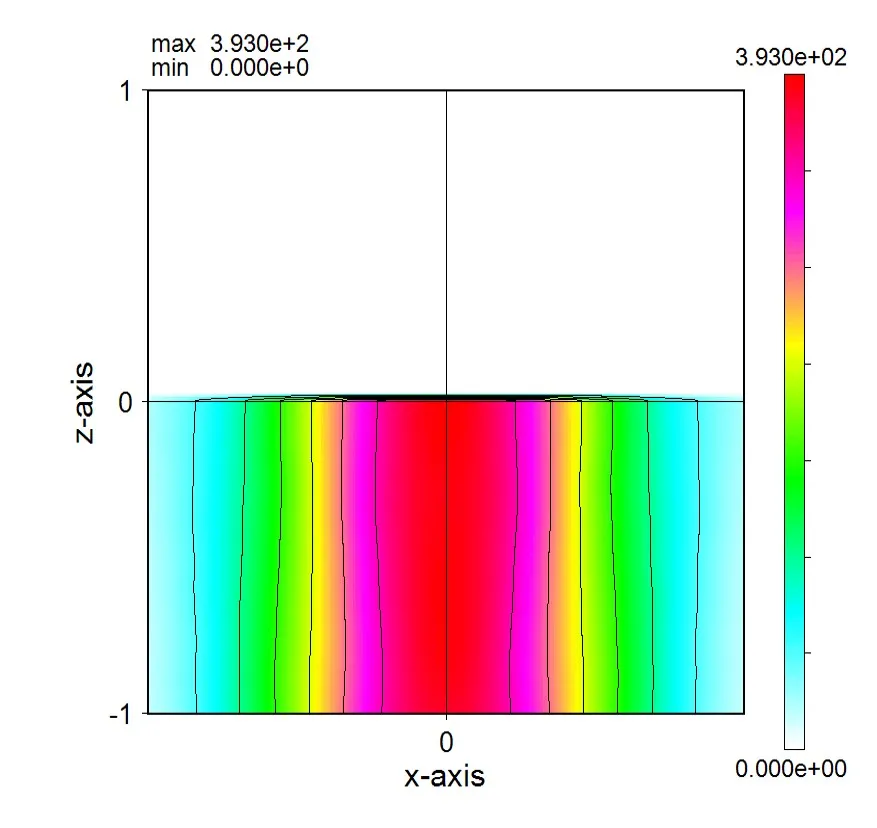
● 光源位置が中間面の場合。
● 下面側の遠方界パターン。
● 上面側の遠方界パターン。
● 各材料領域での計測結果。

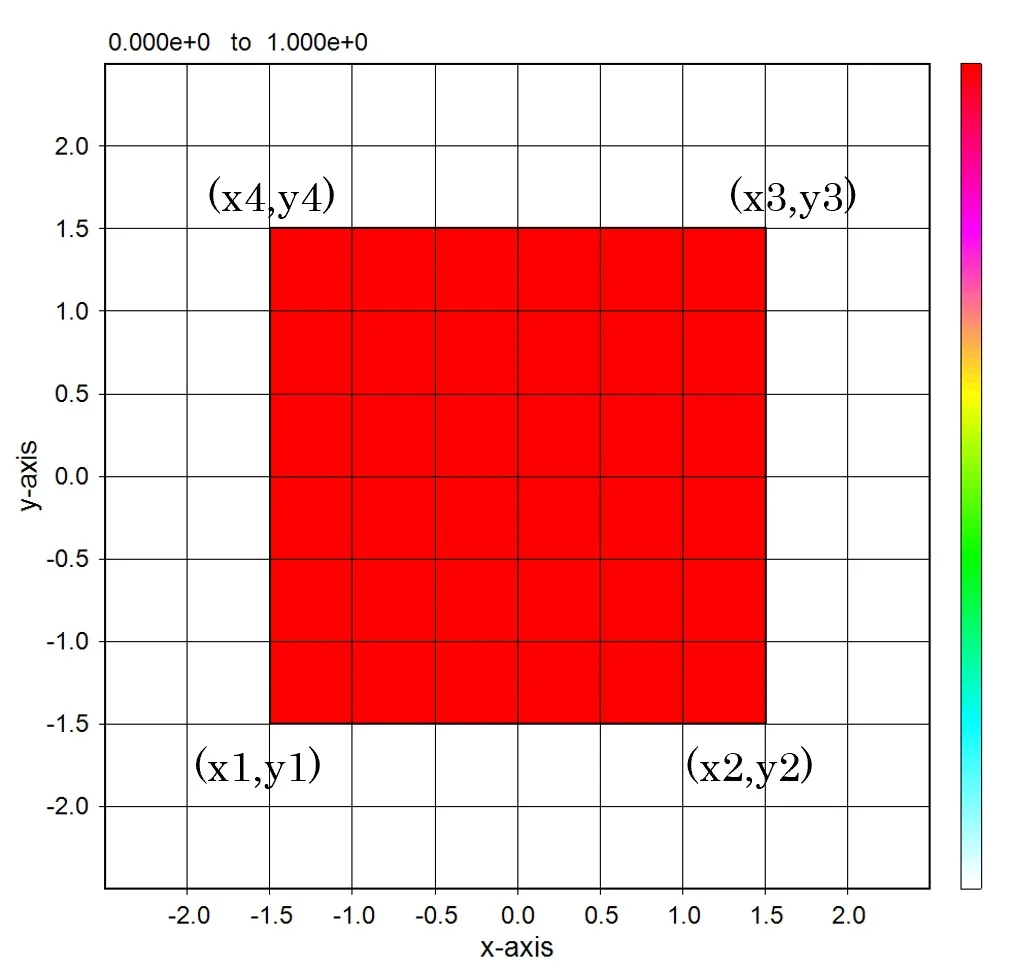
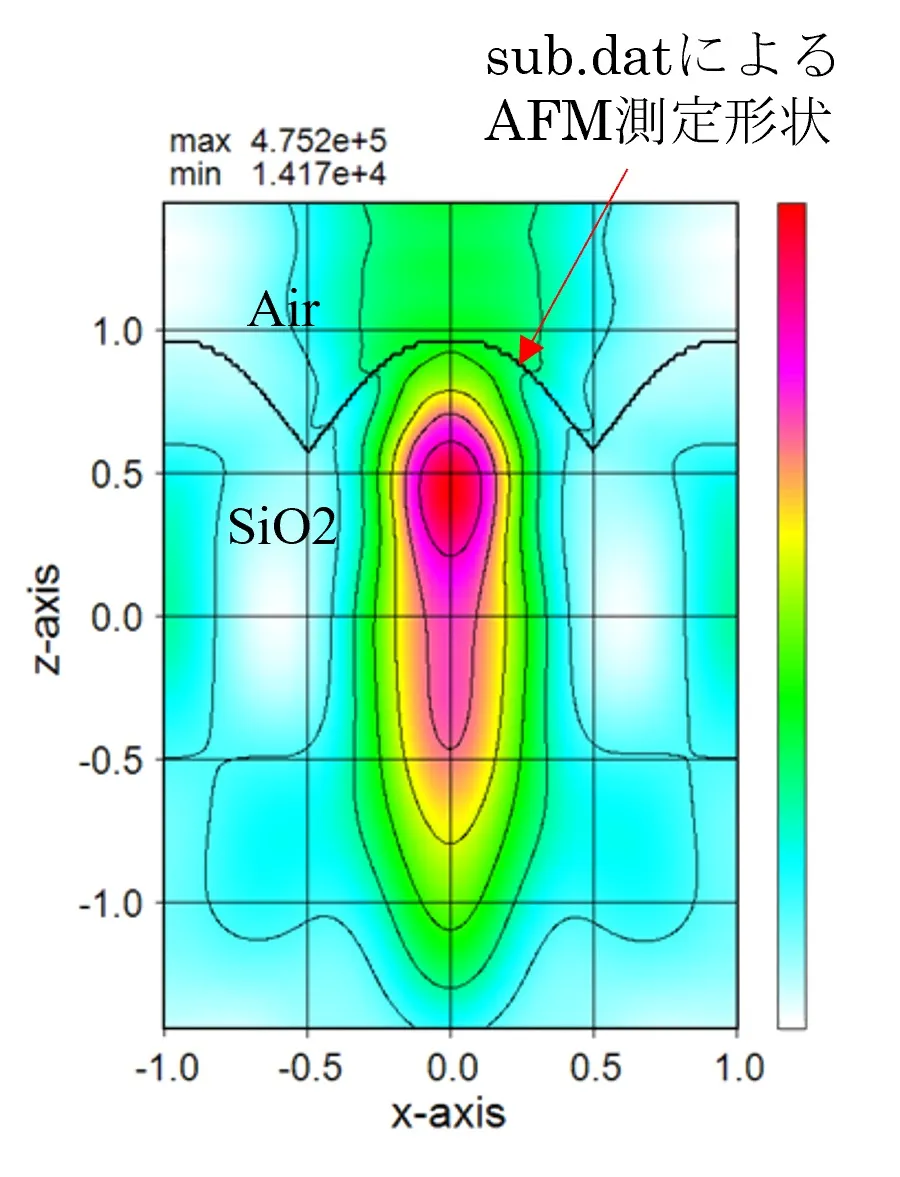
● sub.datを使った外部定義の場合。
sub.datで記述された(x1,y1), (x2,y2), (x3,y3), (x4,y4)の4点の囲む図形が定義できる。
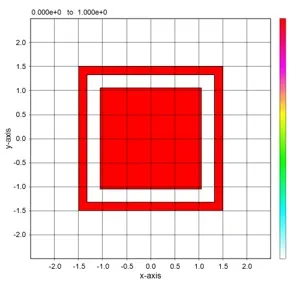
4点データを重ねた場合。これらの周期パターンも簡単に定義できる。
● 外部定義による断面構造の集積によりレンズ形状を表現。
● 上図のモデルに対する回折効率の波長依存性。
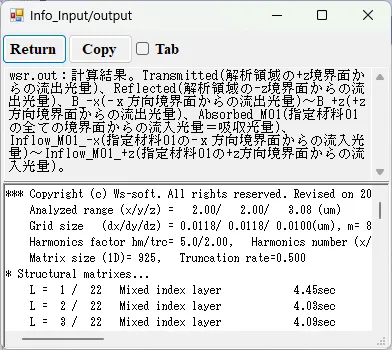
● wsr.out 計算結果。
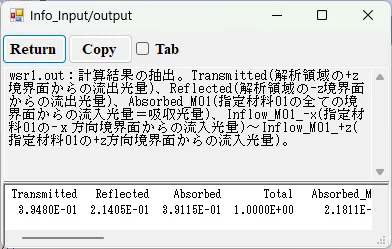
● wsr1.out 計算結果の抽出。
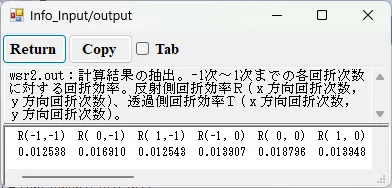
● wsr1.out -1次~1次までの各回折次数に対する回折効率。
● i_xy.out 光強度のxy断面分布。
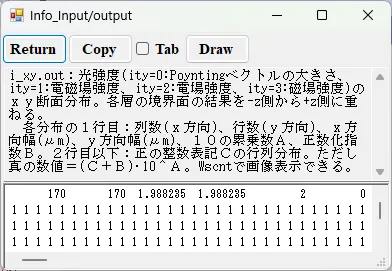
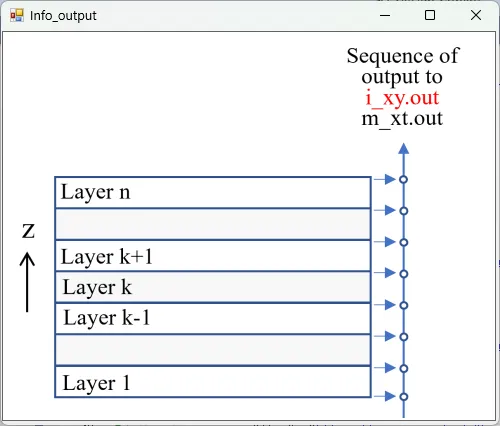
描画例
● i_xz.out 光強度のxz断面(y=csy)の分布。
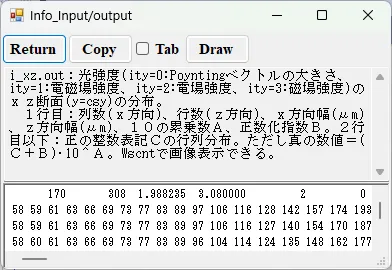
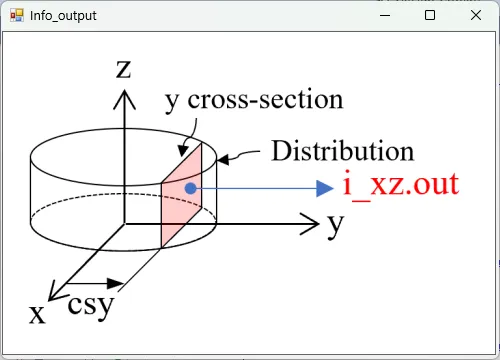
描画例
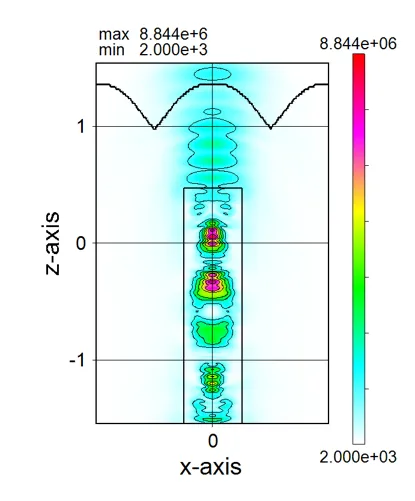
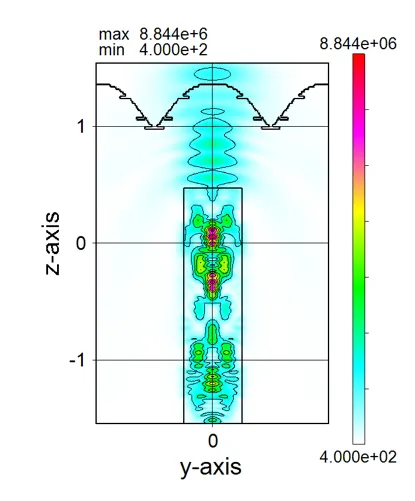
● i_yz.out 光強度のyz断面(x=csx)の分布。
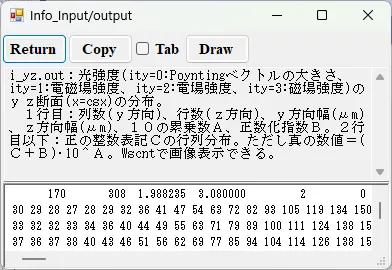
描画例
● i_z045.out 光強度の軸回りに45度回転したz軸断面分布。
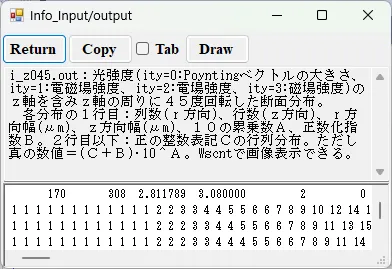
描画例
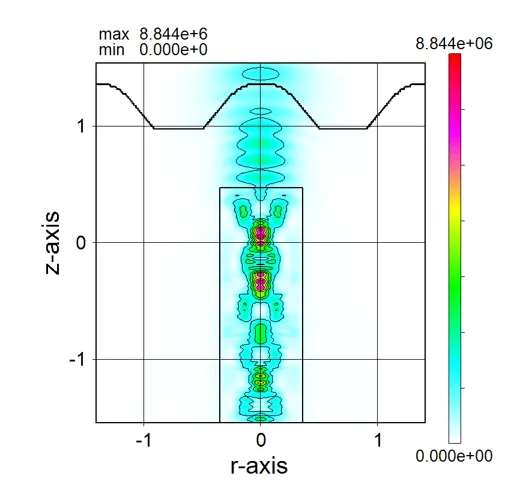
● i_z135.out 光強度の軸回りに135度回転したz軸断面分布。
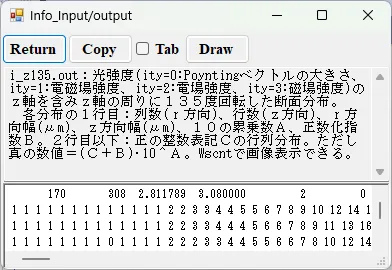
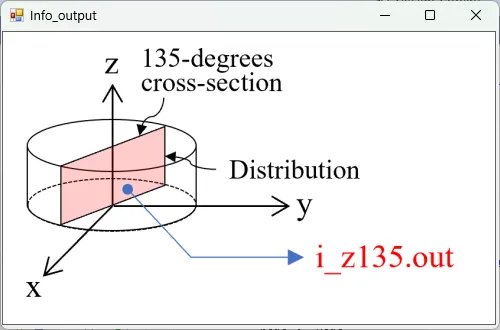
描画例
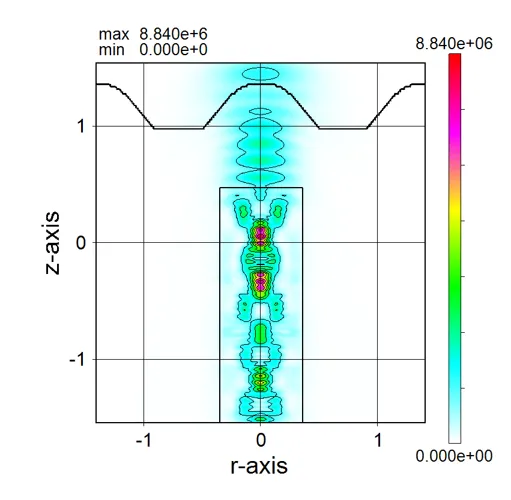
● a_xy.out 光吸収のxy断面分布。
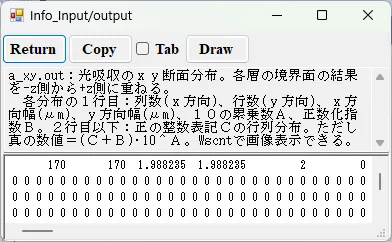

描画例
● a_xz.out 光吸収のxz断面(y=csy)の分布。
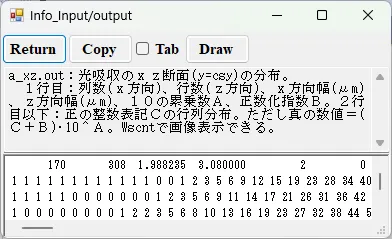
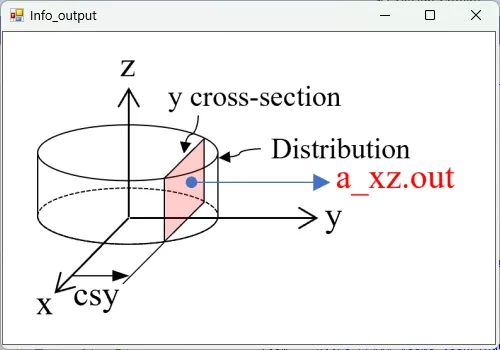
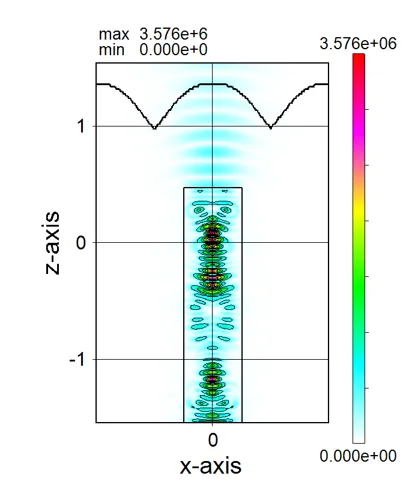
描画例
● a_yz.out 光吸収のyz断面(x=csx)の分布。
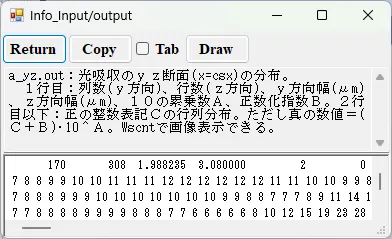
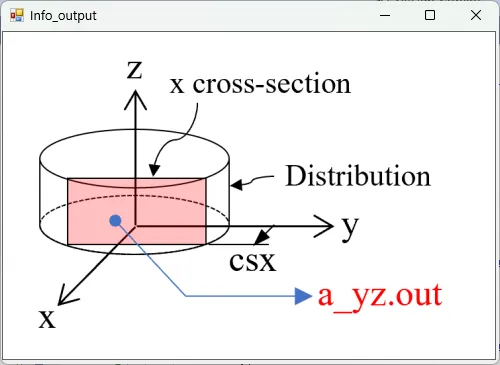
描画例
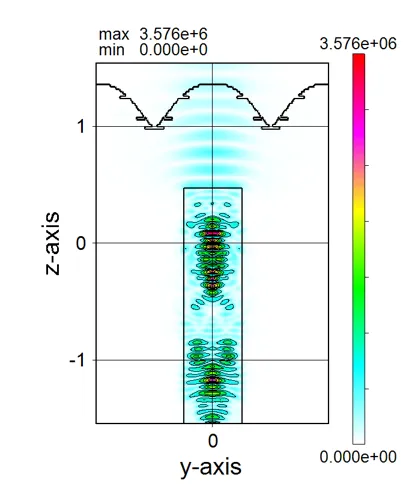
● a_z045.out 光吸収の軸周りに45度回転したz軸断面分布。
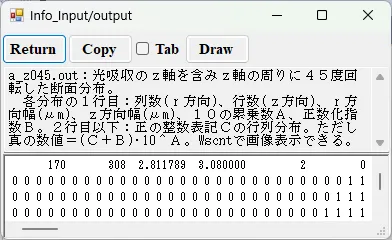
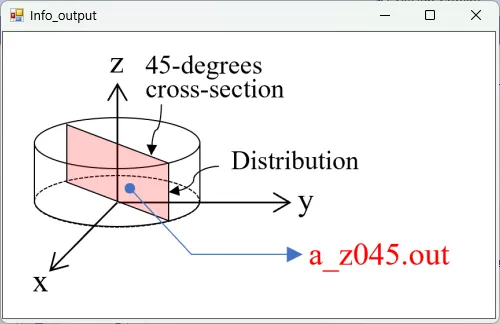
描画例
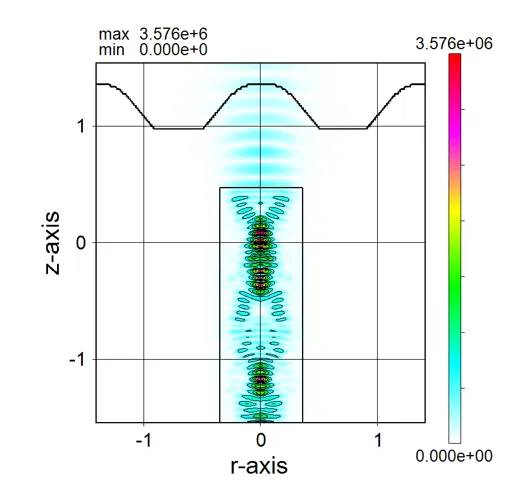
● a_z135.out 光吸収の軸周りに135度回転したz軸断面分布。
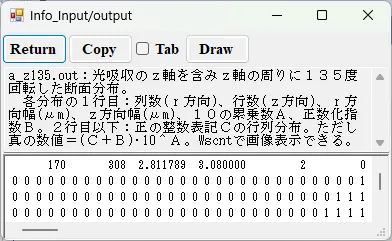
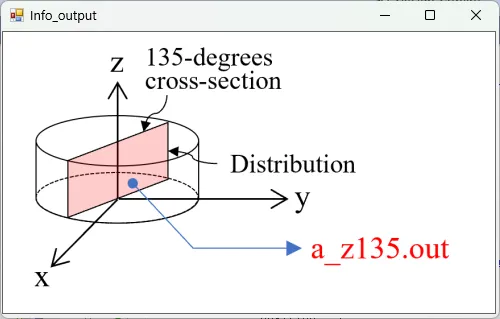
描画例
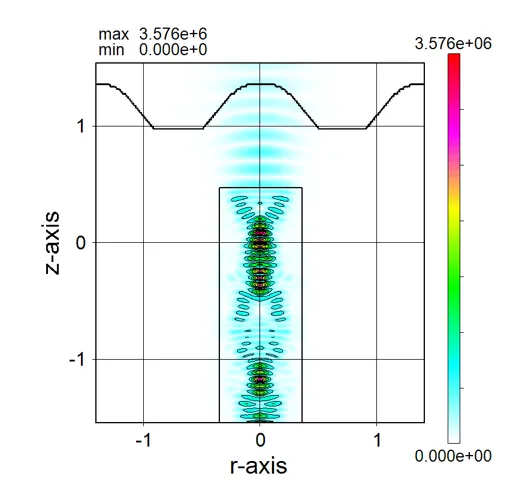
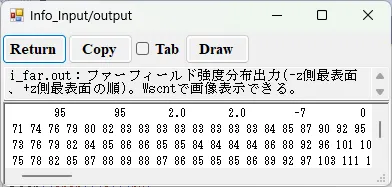
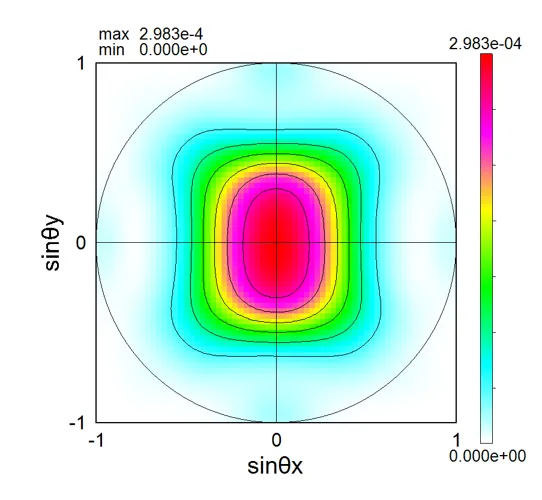
● i_far.out ファーフィールド強度分布出力。
描画例
● eps.out Spatial harmonics分布。
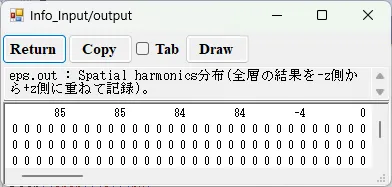
描画例
● 2. hm(Harmonics数比)とtrc(切り捨て係数) New 2025/01/19
● 3. 非周期構造に対応する光源、境界条件
● 4. 光源位置、最上面と任意の中間面
● 5. メモリの圧縮
● 6. 遠方界の計算、下面側と上面側
● 7. 光量計測
● 8. 多彩な断面構造の表現
● 9. レンズ集光の計算
● 10. 回折効率の計算
● 11. 計算結果の可視化
● 12. 出力ファイル
1. 計算原理、フーリエ空間のMaxwell方程式 ▲top
Wsrの計算原理はRCWA(Rigorous coupled-wave analysis)であり、下記(1)~(6)のプロセスを経て、フーリエ空間のMaxwell方程式(Wave Matrix)を解いている。構造がi=1~mのm層からなるとすると(1)~(6)のプロセスは各層において実施される。
(1) 電磁界vectorと格子matrixの定義
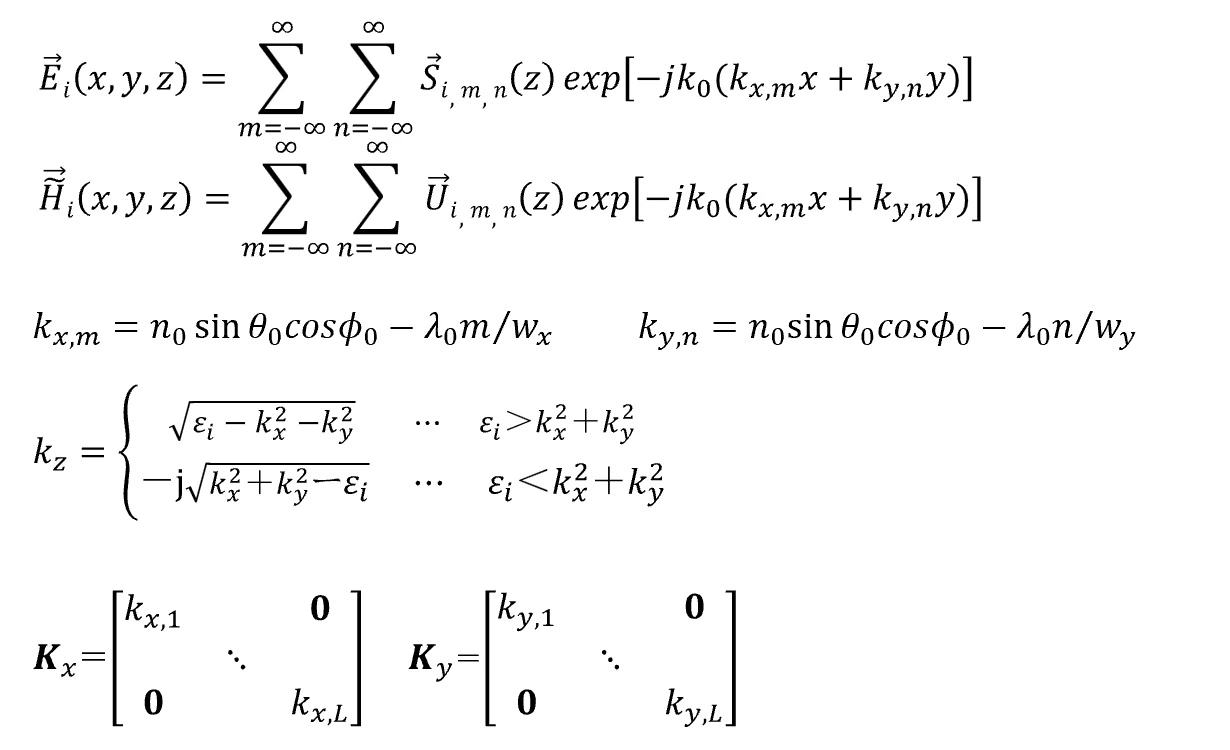
(2) 比誘電率のConvolution matrix計算とmatrixの圧縮
比誘電率分布εi(x,y)の離散フーリエ変換行列の内、中心から(2n+1)×(2n+1)の方形行列を抜き取り、(n+1)2×(n+1)2サイズのConvolution matrixを生成する。抜き取りの形状は円や菱形などに縮小でき、その分Convolution matrixのサイズも大幅に圧縮できる(wsr独自の機能)。wsrではn(Harmonics数)はhm (Harmonics数比)で、抜き取り形状はtrc(切り捨て係数)で設定される。この抜き取りはRCWA法における近似操作に外ならず、計算精度が犠牲になるので演算負荷とのバランスを考慮して決定する必要がある。抜き取りの形状が方形の場合、行列𝑷i, 𝑸i, 𝜴i2, 𝑾iのサイズは2(n+1)2×2(n+1)2となり、波動方程式の行列サイズは4(n+1)2×4(n+1)2になる。演算負荷(メモリ、CPU)は(2n)4に比例する。

(3) 構造matrix計算
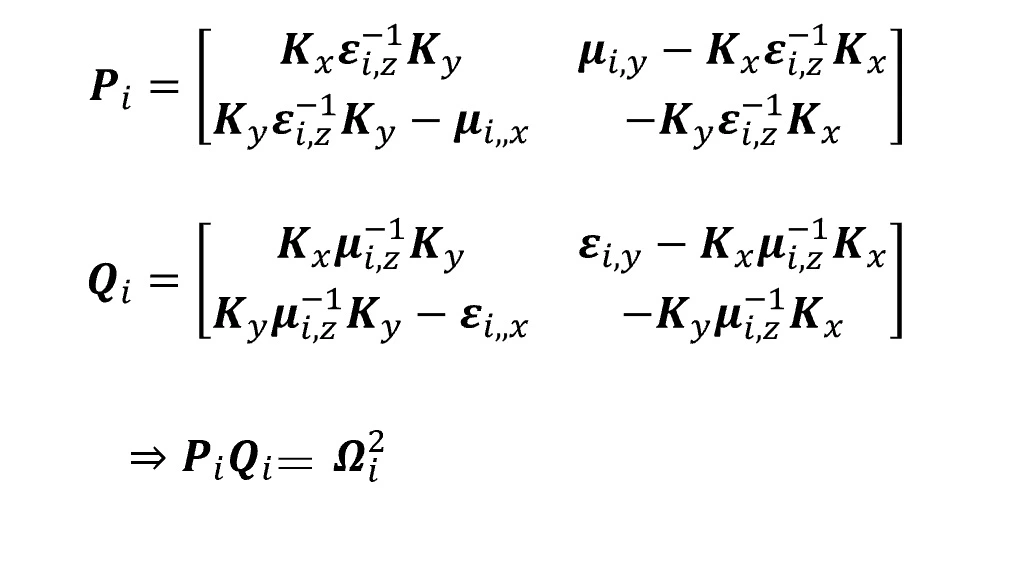
(4) 固有値問題を解く
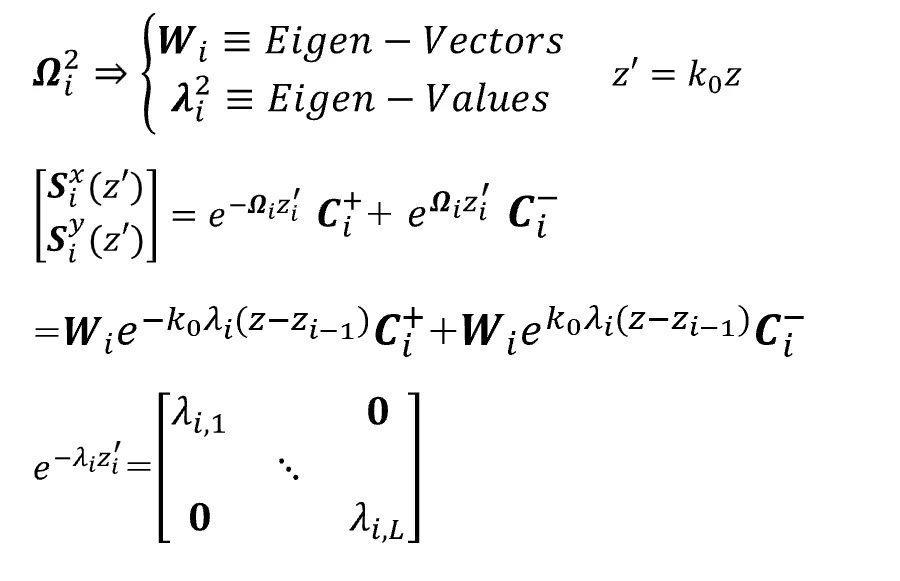
(5) 行列の整列
回折次数を揃えるため固有値λi2の順位を入れ替えて行列を整列させる。

(6) 波動方程式を解く
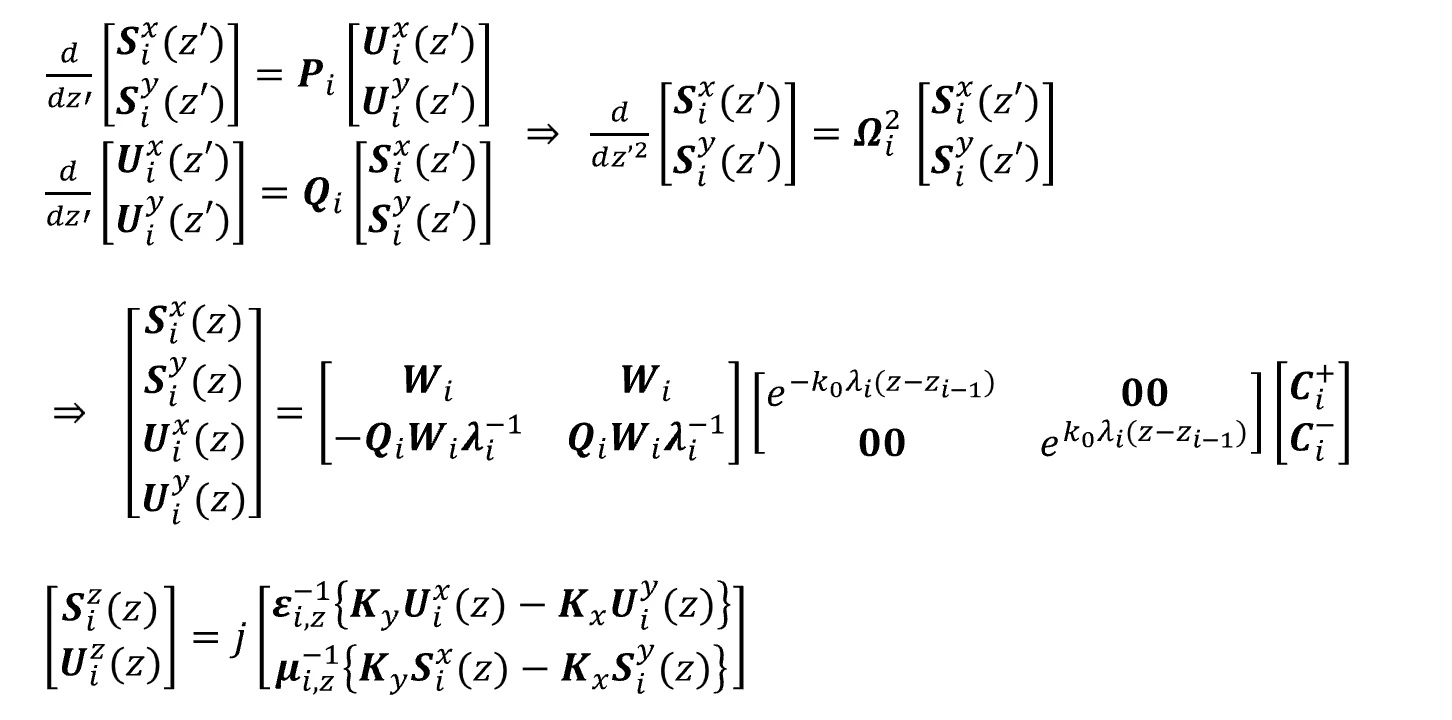
2. hm(Harmonics数比)とtrc(切り捨て係数) ▲top
(1) Convolution matrixの大きさとの関係Harmonics数(整数)をn、波長をλ、解析領域の幅をwとすると、Harmonics数比hmはhm=nw/λで定義される。 Convolution matrixの大きさはn、trc(切り捨て係数)により次式で制限される。 |i/n|2*trc+|j/n|2*trc<1.0
hmが大きいほど、またtrcが小さいほど計算精度は向上するがメモリ消費も増大する(購入前はhmは5以下に制限されている)。
| hm | 5 | 7 | 10 |
|---|---|---|---|
| Matrix size (1D) | 0.71 | 1.00 | 1.43 |
| Matrix size (2D) | 0.712 | 1.00 | 1.432 |
| trc | >10 | 2.0 | 1.0 | 0.0 |
|---|---|---|---|---|
| Truncation shape | ✚ |
◆ |
● |
■ |
| Matrix size (1D) | <0.1 | 0.5 | π/4 | 1.0 |
| Matrix size (2D) | <0.12 | 0.52 | (π/4)2 | 1.0 |
(2) hmと解(透過率)の安定性
下図はtrcを固定して(trc=1.0)、金属円板のモデルでhmに対する解(透過率)の安定性を示す。hmが5以上で安定するが、Harmonics数nが偶数か奇数かで振る舞いに差があり、偶数の方が安定しているのでWsrでは指定しない限り偶数を選んでいる。


下図はtrcを固定して(trc=1.0)、誘電体円板のモデルでhmに対する解(透過率)の安定性を示す。hmが5以上で安定するが、Harmonics数nが偶数か奇数かの差は小さい。


(3) trcと解(透過率)の安定性
下図はhmを固定して(hm=5.0)、金属の円板と方形板を比較したモデルでtrcに対する解(透過率)の安定性を示す。円では3以下、方形では4以下のtrcで解は安定している。


下図はhmを固定して(hm=5.0)、誘電体の円板と方形板を比較したモデルでtrcに対する解(透過率)の安定性を示す。円では3以下、方形では4以下のtrcで解は安定している。


(4) trcとSpatial harmonics分布
円形の構造に対するSpatial harmonics分布(出力eps.out)は等方的な広がりである。

これに対し、方形の構造に対する分布は0度、90度方向に沿って広がる。

従って円形の構造にはtrc=1.0、方形の構造にはtrc=2.0にしても計算精度の劣化は小さく、メモリ消費はそれぞれ0.6倍、0.25倍に圧縮できる。
(5) hmとtrc
hm,trcの設定はConvolution matrixの定義領域を制限するのでRCWA法に於ける近似操作の一つであるが、大幅なメモリ圧縮と演算高速化が可能になる。またhm,trcの適切な設定を行うことで近似誤差を極小化できる。なおtrcによる領域制限はWsr独自の機能であり、市販ソフトの数倍の演算性能を達成できる。
3. 非周期構造に対応する光源、境界条件 ▲top
従来のRCWAでは扱える光源は一様分布で解析境界も周期境界のみであったので、解析対象は反射率、透過率や回折効率の計算等に限定されていた。Wsrは分布光源が扱え吸収境界も配備したので、非周期構造を計算でき、解析対象はFDTD並みに広がっている。● 分布光源で境界条件が周期境界条件(PBC)の場合。

● 分布光源で境界条件が吸収境界条件(ABC)の場合。

4. 光源位置、最上面と任意の中間面 ▲top
従来のRCWAでは光源位置は最上面のみであったが、Wsrではz方向の任意位置に設置できる。● 光源位置が最上面の場合。

● 光源位置が中間面の場合。

5. メモリの圧縮 ▲top
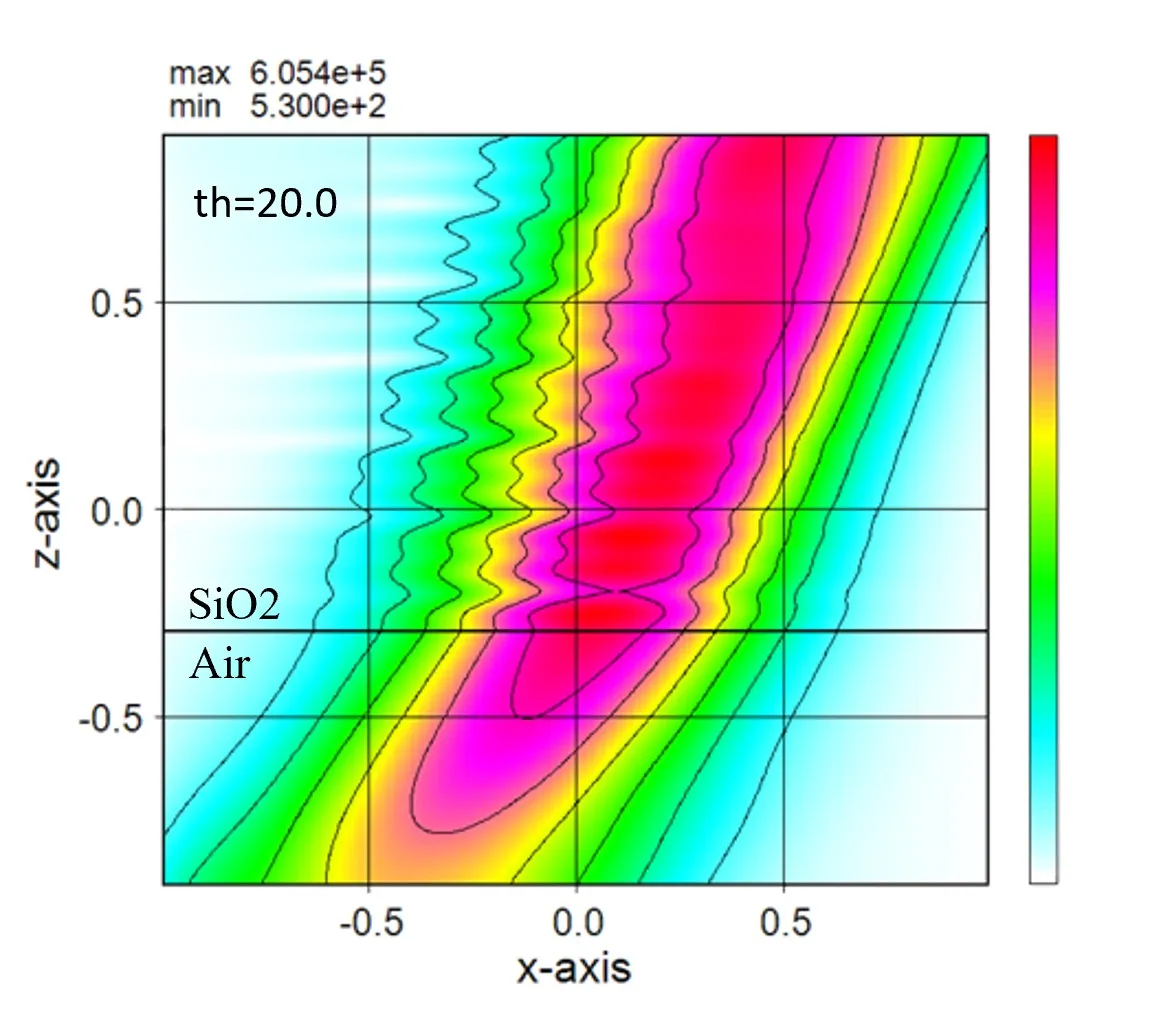
RCWAの欠点は消費メモリが大きいことにあるが、Wsrではメモリ消費を極限まで圧縮している。例えば、層内が均質な媒質の比誘電率分布は疎行列の表現になるので、その分のメモリは圧縮される。また切り捨て係数trcの採用で行列サイズは圧縮され、メモリ消費を1/4以下にできる。メモリ圧縮に比例し、演算速度は増大する。6. 遠方界の計算、下面側と上面側 ▲top
● 下図のモデルで上下面方向の遠方界が計算される。
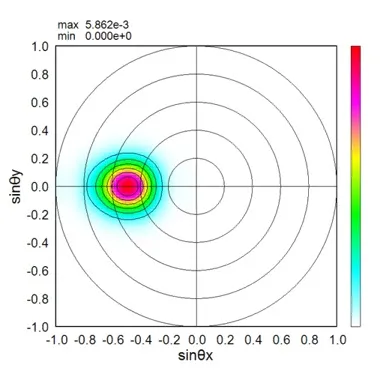
● 下面側の遠方界パターン。

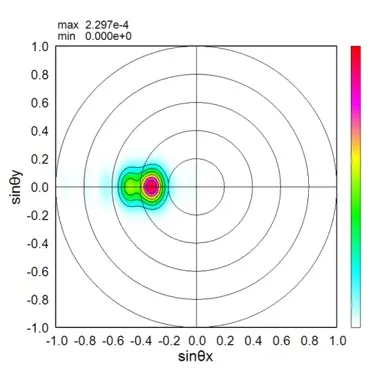
● 上面側の遠方界パターン。

7. 光量計測 ▲top
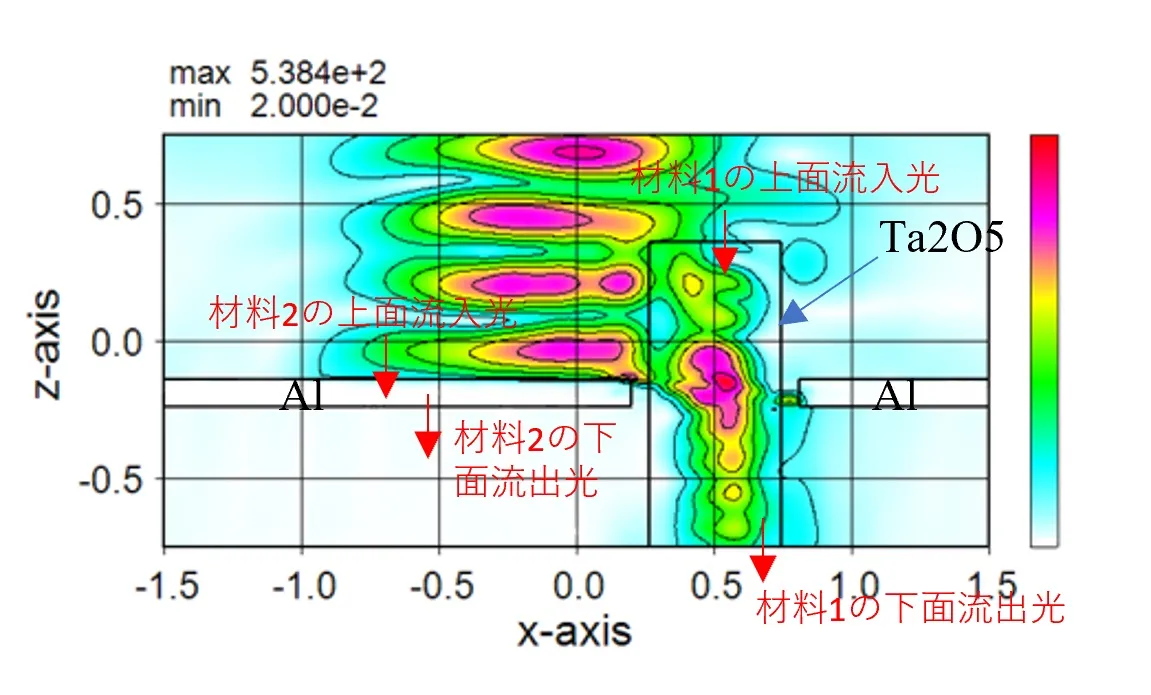
● 各材料や領域の入出光量や吸収光量が個別に計測できる。
● 各材料領域での計測結果。
8. 多彩な断面構造の表現 ▲top
● 内部定義の場合。
● sub.datを使った外部定義の場合。
sub.datで記述された(x1,y1), (x2,y2), (x3,y3), (x4,y4)の4点の囲む図形が定義できる。

4点データを重ねた場合。これらの周期パターンも簡単に定義できる。

9. レンズ集光の計算 ▲top
● 内部定義による円構造の集積によりレンズ形状を表現。
● 外部定義による断面構造の集積によりレンズ形状を表現。

10. 回折効率の計算 ▲top
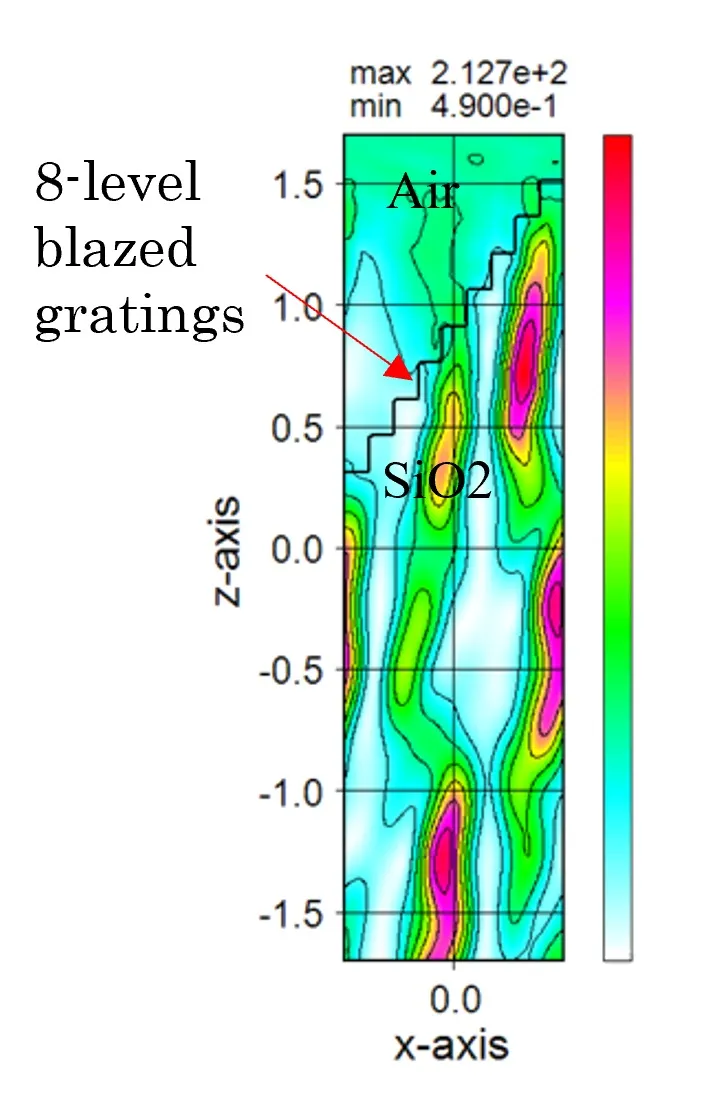
● 8レベルの回折格子に対する一様強度入射、周期境界条件での光強度分布。
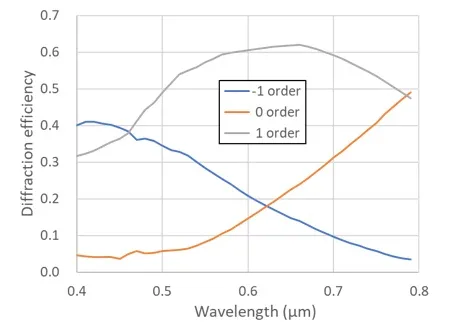
● 上図のモデルに対する回折効率の波長依存性。

11. 計算結果の可視化 ▲top
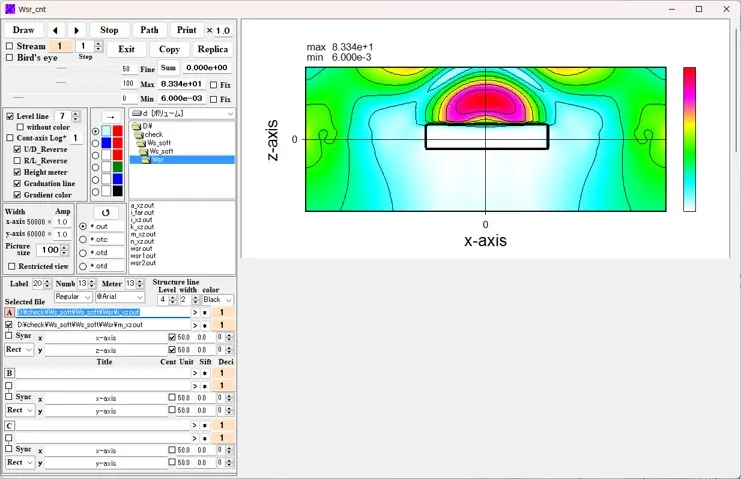
● 実行時にWscntにより強度分布をリアルタイムに表示。
12. 出力ファイル ▲top
Source setting画面の結果ファイルボックス内の項目をダブルクリックすることで表示される内容を基に、各出力ファイルの内容を説明する。
● wsr.out 計算結果。

● wsr1.out 計算結果の抽出。

● wsr1.out -1次~1次までの各回折次数に対する回折効率。

● i_xy.out 光強度のxy断面分布。


描画例
● i_xz.out 光強度のxz断面(y=csy)の分布。


描画例

● i_yz.out 光強度のyz断面(x=csx)の分布。


描画例

● i_z045.out 光強度の軸回りに45度回転したz軸断面分布。


描画例

● i_z135.out 光強度の軸回りに135度回転したz軸断面分布。


描画例

● a_xy.out 光吸収のxy断面分布。


描画例
● a_xz.out 光吸収のxz断面(y=csy)の分布。


描画例

● a_yz.out 光吸収のyz断面(x=csx)の分布。


描画例

● a_z045.out 光吸収の軸周りに45度回転したz軸断面分布。


描画例

● a_z135.out 光吸収の軸周りに135度回転したz軸断面分布。


描画例

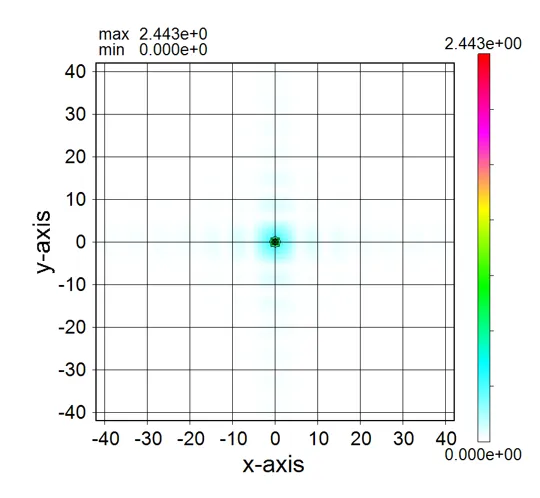
● i_far.out ファーフィールド強度分布出力。

描画例

● eps.out Spatial harmonics分布。

描画例
